Математика кофеварок

Привет. Хочу поделиться удовольствием от решения практической задачи, на которую я потратил несколько вечеров. А ещё, возможно, какой-то владелец кофейни воспользуется моим решением для упрощения своей работы.

Суть задачи

В кофейне есть 5 разных видов стаканов: 0,2; 0,3; 0,4 бумажные для горячих напитков и 0,3; 0,4 пластиковые для холодных напитков. Эти стаканы расходуются с разной скоростью. Как быстро? Это мы можем установить из статистики продаж напитков, например, за пару последних месяцев.

В кофейне есть 3 вида крышек. 80 мм на стаканы 0,2; 90 мм на стаканы 0,3 и 0,4; пластиковые крышки на пластиковые стаканы. При этом крышки тратятся чуть медленнее, чем стаканы, так как иногда ими не пользуются (примерно 95 крышек уходит на 100 стаканов).

После инвентаризации мы знаем остаток стаканов и крышек на складе. Мы знаем цену каждой позиции у поставщика. Заказываем мы стаканы на какую-то сумму, каждый раз разную, зависящую от ряда причин. Это может быть, как 20.000, так и 50.000 рублей.

Вопрос

Сколько нужно заказать каждых стаканов и крышек, чтобы они закончились одновременно, а поставщик выставил счёт на определённую сумму.

Зачем решать эту задачу

Почему вообще крышки и стаканы должны заканчиваться одновременно? Ну, закажи ты по 1000 штук из каждой позиции, и всё.

Нет. Это приведёт к тому, что каких-то позиций будет очень много, а какие-то нужно будет уже заказывать. Что, во-первых, замораживает деньги на долгое время, во-вторых, нецелесообразно перегружает складские помещения.

Как я решал эту проблему раньше? На самом деле, видя условия задачи, я всегда очень быстро подбором угадывал необходимое число каждых позиций для заказа. Проблемы начались, когда эту задачу делегировали старшим бариста. Каждый старший бариста должен сформировать заказ для своей кофейни на определённую сумму, после заказы из всех кофеен объединяются в один большой заказ, который и направляется поставщику.

Оказалось, иногда невозможно объяснить на пальцах кому-то что-то, что решается логическим подбором, если нет однозначного алгоритма вычислений. Ну тогда, подумал я, сейчас в Excel’е быстро накидаю таблицу для создания таких заказов, логика действий же очевидна.

Потратив полвечера на создание таблицы и не получив хорошо работающей модели, я осознал, что задача несколько сложнее чем кажется, и без математической составляющей её не решить.

Система уравнений

Тогда я взял тетрадку и ручку, чтобы попытаться составить систему уравнений из всей доступной информации. Для начала я назначил буквы всем параметрам. Например, a – цена бумажного стакана 0,2, b – 0,3, а h – крышек для пластиковых стаканов.

Далее начал составлять уравнения. Главное уравнение – произведение стаканов и крышек, которые есть на складе и которые закажем на их цену равно сумме заказа и ценового эквивалента тех позиций, которые есть на складе.

Теперь попытаемся всё выразить, например, через X1 – требуемо число бумажных стаканов 0,2. Что мы ещё знаем? Мы знаем, каким должно быть отношение числа всех стаканов после заказа друг к другу. Так мы можем выразить X2, X3, X4, X5 через X1.

Теперь с крышками. Умножаем число имеющихся и тех, что закажем стаканов, для которых предназначена данная крышка, на соответствующий коэффициент (0,95). Вычитаем имеющиеся крышки на складе. Выражаем всё через X1. Подставляем всё в главное уравнение, получаем уравнение с 1 неизвестным – X1.

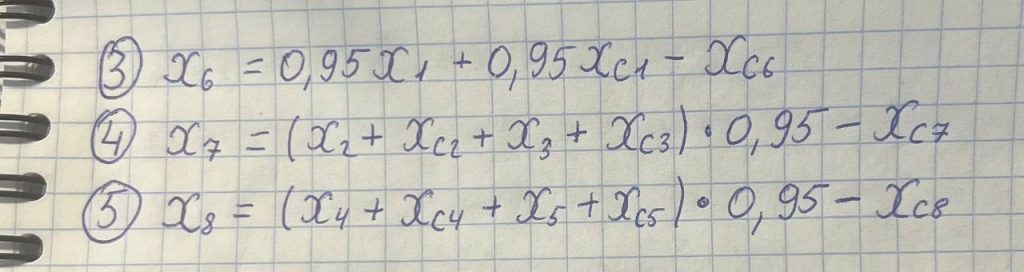
Подставляем всё в главное уравнение, получаем уравнение с 1 неизвестным – X1.

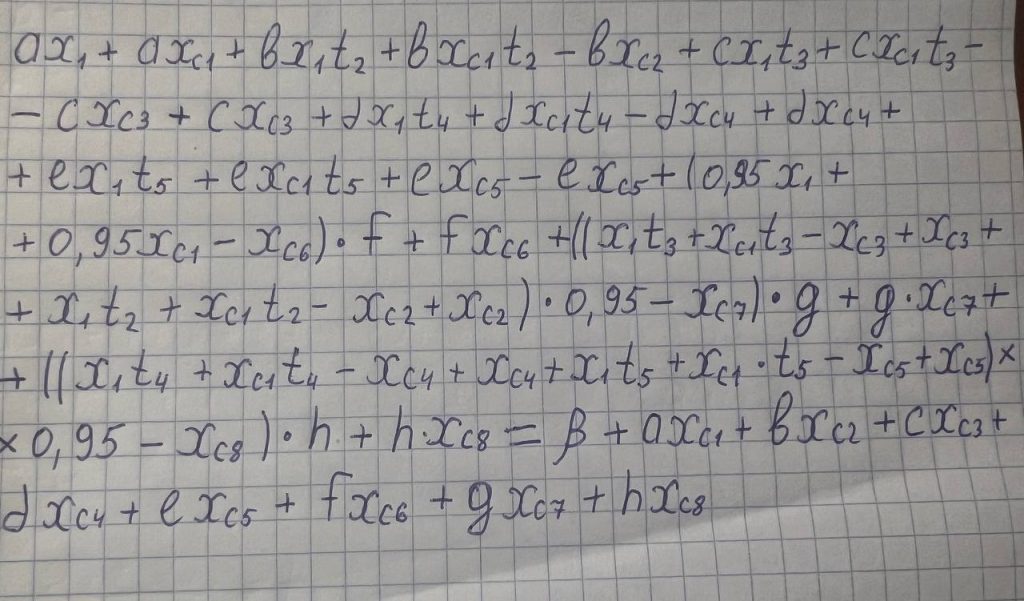
К слову, проще было бы решить задачу для меньшего разнообразия позиций, а потом по аналогии добавить, но понял я это слишком поздно.

Теперь выражаем X1, попутно производим все необходимые преобразования. Получаем элегантное уравнение зависимости числа стаканов 0,2 от всех остальных показателей.

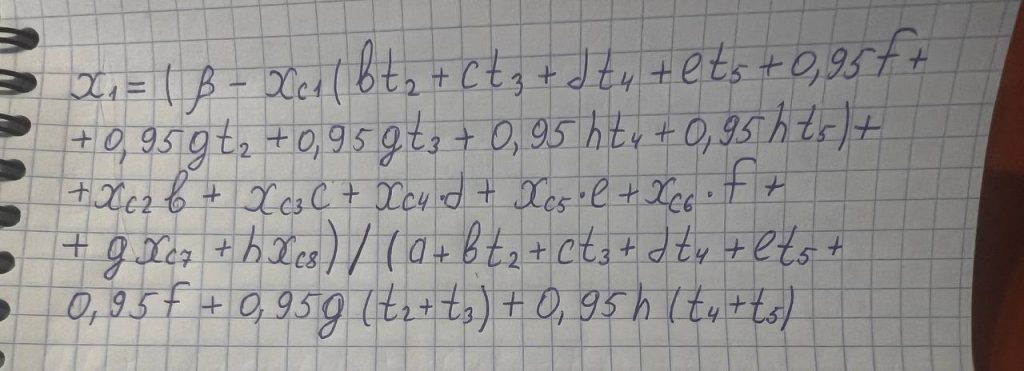
Зная X1, мы можем легко выразить X2, X3, X4, X5, X6, X7, X8 из приведённых выше уравнений.

Теперь создать таблицу Excel проще простого. Вбиваем имеющиеся значения, и таблица всё считает сама. Делаем так, чтобы значения округлялись до кратных числу стаканов или крышек в упаковке.

Недостатки

В чём недостатки модели? Если каких-то позиций слишком много на складе, а сумма заказа маленькая, X может принимать отрицательные значения. Это значит, что в реальной ситуации нам бы пришлось вернуть излишки со склада поставщику и потребовать за них деньги, что выглядит глупо. Изначально я думал ещё больше доработать функцию, чтобы она вела пересчёт в случае отрицательных X. Но когда подставил рабочие значения, то понял, что в используемых условиях данной модели более чем достаточно, если через логическую функцию занулить отрицательный X.

Вместо заключения

Теперь у меня есть отлично работающая система для расчёта стаканов, которую можно использовать при масштабировании, а ты, можешь гордиться своей выдержкой, если дочитал до этого момента.